| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 스프링 기초
- 프로그래밍언어
- JShell
- 초보코딩탈출
- 기초코딩
- Git
- 자바 스프링
- 자바
- 프로그래밍기초
- 배열
- spring
- 클래스
- 제이쉘
- 이클립스
- 초보코딩
- 데이터베이스
- 스프링
- 컴퓨터과학개론
- github
- eclips
- Java
- 코딩초보
- JAVA기초
- 메소드
- 리눅스
- 자바기초
- Elk
- 프로그래밍
- 알고리즘
- 자바프로그래밍
- Today
- Total
키보드워리어
【컴퓨터과학개론】트리에 대해서 본문
안녕하세요 【키보드 워리어】
⌨🗡🧑
블로그 방문자 여러분, 안경닦이입니다.
이진트리 | 완전 이진트리 | 포화 이진트리
트리부터 살펴봅시다 트리는 노드(node)라고 불리는 부분과 노드를 연결하는 가지(branch)로 구성되며, 노드 사이에는 나무뿌리 모양의 데이터의 계층적인 관계성을 갖습니다
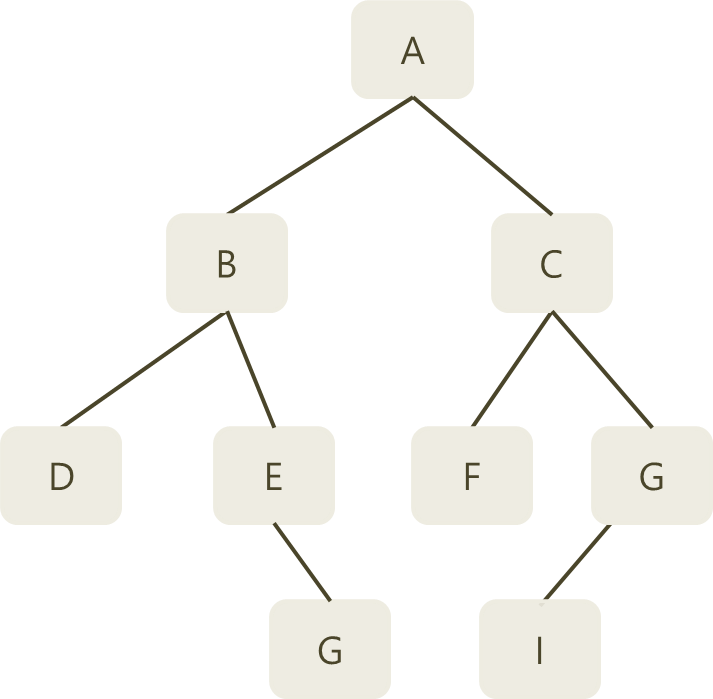
각 노드에 있는 가지의 수를 차수(degree)라고 하며 트리의 차수란 모든 노드의 차수 중에서 제일 큰 차수를 의미하는데요 그렇다면 이진트리는(binary tree) 무슨 의미가 되나요?
트리 중에서 차수가 2인 트리를 의미하며, 모든 노드의 차수는 최대 2를 넘지 않는 것이 이진트리입니다
이진트리의 모든 노드는 최대 두 개의 서브 트리를 가지며, 각 서브트리는 왼쪽 서브 트리와 오른쪽 서브 트리로 구분됩니다
이진트리는 왼쪽과 오른쪽 노드에 ‘순서’의 의미를 부여해주어요 그리고 이진 트리의 각 서브 트리는 다시 이진트리가 됩니다 이러한 이진트리의 특성을 이용하면, N개의 노드를 가진 이진트리의 최대 높이와 최소 높이를 구할 수 있습니다
이진트리의 연산으로는 삽입, 삭제, 순회가 있고 여기서 순회란 일정한 순서에 따라 트리에 있는 각 노드를 한 번씩 방문하는 걸 의미합니다 그리고 순회 연산을 이용하면 트리 내의 정보를 선형적인 순서의 정보로 만들 수 있게 됩니다
트리가 데이터를 나타내는 루트 노드(D), 왼쪽 서브트리 (L), 그리고 오른쪽 서브 트리로 간단히 구성되어 있다고 한다면 모두 여섯 가지의 서로 다른 방문 순서로는 LDR, RDL, LRD, RLD, DLR, DRL을 얻을 수 있습니다
왼쪽 서브 트리와 오른쪽 서브 트리를 방문하기 전에 먼저 루트 노드를 방문하면 전위 순회, 왼쪽 서브 트리와 오른쪽 서브 트리 중간에 루트 노드를 방문하면 중위 순회, 그리고 왼쪽 서브 트리와 오른쪽 서브 트리를 모두 방문한 다음에 루트 노드를 방문하면 후위 순회가 됩니다
그렇다면 포화, 완전 이진트리와 같이 특수한 조건을 갖는 이진트리는 과연 무엇일까요?
먼저 포화 이진트리(Full binary tree)란 깊이가 k인 이진트리 중에서 노드의 개수가 2k승 -1개인 이진트리를 의미합니다
다시 말해, 깊이가 k인 이진트리가 가질 수 있는 노드의 최대 개수는 2k승 -1이며, 단말 노드의 개수가 2k승 -1개를 의미합니다 모든 내부 노드들은 두 개의 자식 노드를 갖는데 예를 들어 깊이가 8이면 2의 8승 256-1, 255개가 되는 겁니다!
그래서 포화 이진트리는 각 레벨에서 빈자리가 없이 노드를 모두 가지고 있어야 하는 거예요
(레벨이 7까지 모두 빈자리 없이 총 2의 8 승개의 노드로 채워집니다)
완전 이진트리(Complete binary tree)는 트리의 최대 레벨이 k일 때, 레벨 k-1까지는 포화 이진트리를 형성하고, 레벨 k에서는 왼쪽부터 오른쪽으로 채워진 트리입니다
앞서 살펴본 포화 이진트리의 경우에는 루트 노드로 시작해서 레벨별로 오른쪽으로 번호를 부여할 수 있고, 완전 이진트리는 총노드의 개수가 (2k+1승 -1)을 초과하지 않으면서 포화 이진트리의 번호와 일치하는 이진트리를 의미한다.
'Universirty > 1-2' 카테고리의 다른 글
| 【컴퓨터과학개론】종합 정리 기출문제 - 1 (0) | 2022.09.29 |
|---|---|
| 【컴퓨터과학개론】조합회로와 순차회로 (0) | 2022.09.22 |
| 【컴퓨터과학개론】가상 기억장치의 페이징 기법과 세그먼테이션 기법 (0) | 2022.09.19 |
| 【컴퓨터과학개론】정렬 알고리즘 (0) | 2022.09.17 |
| 【컴퓨터과학개론】정수와 실수의 표현 방법 (0) | 2022.09.15 |


